Hello everyone and welcome to my new post!
In the previous article, we implemented a simple solution for a code problem. Make sure to read it to learn about the task and the algorithm we have at the moment.
Today, we are going to look at how we can enhance it. Let’s go, it will be fun!
Existing solution
Current solution offers us time and space complexity both of \(O(N^3)\).
This is a quite high value. It means that with bigger input strings it will take significantly more time to calculate the result. The memory needed to store the internal set of substrings will also grow dramatically. Can we do anything with it?
Think about areas to improve
Space
In terms of space, the main source of memory consumption is the ancillary substring set. Ideally, we would like to get rid of it. This is possible if we change our implementation to not collect the substrings.
We can achieve this by introducing a new variable for tracking the current maximum substring length and checking length for new substrings as soon as we generate them. Here is how our implementation can look like.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public class Solution {
public static int lengthOfLongestSubstring(String input) {
int maxLength = 0;
for (int beginIndex = 0; beginIndex < input.length(); beginIndex++) {
for (int endIndex = beginIndex; endIndex < input.length(); endIndex++) {
String substring = input.substring(beginIndex, endIndex + 1);
if (hasOnlyUniqueChars(substring) && substring.length() > maxLength) {
maxLength = substring.length();
}
}
}
return maxLength;
}
private static boolean hasOnlyUniqueChars(String substring) {
// ...
}
}
Such approach replaces the internal substring set with one simple integer variable for storing the maximum length. The integer will always require \(O(1)\) memory. Apart from that, we still have a call to hasOnlyUniqueChars which at any point of execution will use not more than \(O(N)\) space.
Time
If we run the current solution with huge inputs of a couple of thousands length, the execution time will grow to a couple of seconds. That’s too much.
Let’s carry out an analysis of the current approach.
As discussed in the previous article, this will be the substrings found on the first outer loop iteration for the input string ababcdww: a, ab, aba, abab, ababc, ababcd, ababcdw and ababcdww.
If we think about it, there is no point in looking for further substrings once we know that aba has letter a duplicated. That is, every substring starting with aba will have duplicates. So really the first iteration should check only a, ab and aba, and skip the rest.
The same is valid for the second iteration. Instead of checking b, ba, bab, babc, babcd, babcdw, babcdww, it should only try until the first duplicate is found. Thus, it needs only these three b, ba and bab.
We could incorporate this change by utilizing break keyword in the inner loop. However, there is a way that suites better to this logic. Let’s take a look at it in the next chapter.
New algorithm
The updated approach will actually do what a human would. You would not continue creating new substrings on top of one which already has duplicates, would you? :)
We can implement this with something called two pointers. The pointers will mark the start and the end of each substring, and the main difference will be that we will use a while-loop instead of nested for-loops.
At first, we want to start with substring a, so both pointers will mark the first letter as the start and the stop letter. Next, we move the end pointer one letter to the right (start is the first letter, stop is the second one) and we get substring ab. On each this step we track the current maximum length.
As soon as we hit the first duplicate letter (substring aba), we want to resolve the duplicates first before continuing expansion to the right. How do we resolve it?
Well, we move the start pointer to the right, until we eliminate the most left letters including the left duplicate. We know this way we don’t skip anything important. We have already considered substrings with letters to the left, and there will be no further use of them as they don’t allow to generate new valid substrings.
We can repeat this process until the end pointer reaches the last letter of the input string. Now all next substrings can only be shorter. Thus, the algorithm can be safely stopped.
Already eager to see some visualization? Here you go! 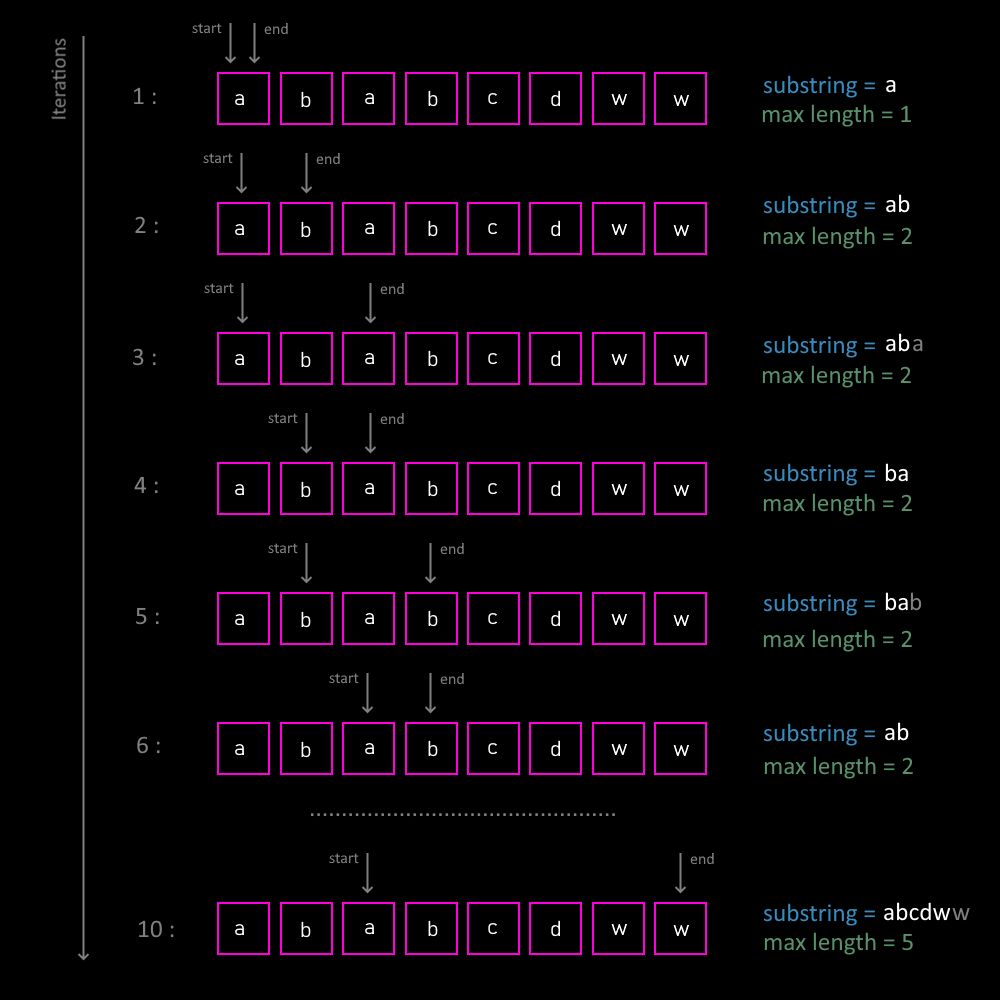
Let’s put the full code for this solution together.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public class Solution {
public static int lengthOfLongestSubstring(String input) {
int maxLength = 0;
int start = 0;
int end = 0;
while (end < input.length()) {
String substring = input.substring(start, end + 1);
if (hasOnlyUniqueChars(substring)) {
if (substring.length() > maxLength) {
maxLength = substring.length();
}
end++;
} else {
start++;
}
}
return maxLength;
}
private static boolean hasOnlyUniqueChars(String substring) {
char[] stringChars = substring.toCharArray();
Set<Character> uniqueChars = new HashSet<>();
for (char stringChar : stringChars) {
uniqueChars.add(stringChar);
}
return stringChars.length == uniqueChars.size();
}
}
Algorithm complexity
Now that we have the new implementation in place, we can see its impact on efficiency.
Time
To determine the time complexity, we need to assess how the number of actions changes depending on the input. Actions in our approach are done for each move of a pointer.
Each of the pointers can do at max N steps moving along the input string. These steps will also call hasOnlyUniqueChars which in turn makes \(O(N)\) operations. This gives us \((O(N) + O(N)) * O(N) = O(2N) * O(N) = O(2N^2)\), which, as we already know, results in \(O(N^2)\) in the world of complexity.
Space
Here we utilize the improvement discussed above. We replace the set with one integer variable to store the max length. And the main part consuming memory now is hasOnlyUniqueChars method. Overall space complexity is \(O(N)\).
Conclusion
We have significantly improved our code in terms of both time and space. The method of two pointers enabled us to decrease the time complexity from \(O(N^3)\) to \(O(N^2)\), which is a noticeable improvement. The space complexity now moved from \(O(N^3)\) to \(O(N)\), and this is also a huge step forward. This change came with an updated logic that probably needs a little bit more time to understand. However, this is 100% worth it, as the new version of our program is much more resilient.
Running a couple of measurements shows us that the new version can easily handle strings of tens of thousand of characters, while the initial version gets very slow at something after two thousands.
That’s all for today, hope you enjoyed it. Have a good day and see you next time!